Basic proportionality Theorem

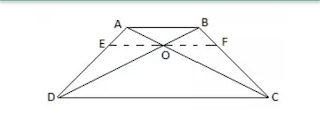
Sum No.10:- T he diagonals of  a quadrilateral ABCD intersect each other at a point O such that AO/BO=CO/DO. show that ABCD is a trapezium. Solution:- Given :- ABCD is a quadrilateral, whose diagonals AC and BD intesect each other at O. such that AO/BO=CO/DO i.e., AO/CO=BO/DO......(1) To prove :- ABCD is a trapezium. Construction :- from O,draw OE∥AB. Proof :- In △ADB, we have,              OE∥AB (construction) ∴ by BPT, we have  AE/ED=BO/DO.....(2) from (1) and (2),we have AO/CO=AE/ED thus in △ADC,E and O are points dividing the sides AD and AC in the same ratio. ∴ by converse of BPT, we have {OE∥CD but OE∥AB by construction} hence OE∥CD∥AB ⇒ AB∥CD ∴ Quadrilatral ABCD is at Trapezium.

                                              EXERCISE 6.2 SUM NO.9 ABCD is trapezium in which AB∥DC and its diagonals intersect each other at the point O.show that AO/BO=CO/DO. Solution:-   Given :-In trapezium ABCD,AB∥DC, diagonal AC and BD intersect at o. Construction:- Draw OE∥DC, intersecting AD at E. Proof:- in △ ADC, OE∥DC(by construction)    ∴ AE/ED=AO/OC......(1)          (by Basic proportionality theorem) Again,in △ABD,OE∥A B AE/ED=BO/OD.....(2) [∵ OE∥ DC (by construction) and DC∥AB (given) also by  by Basic proportionality theorem )  From (1) and (2) we have: AO/CO=BO/OD AO/BO=CO/DO Hence proved

  Exercise 6.2 Question 1:-   Solution:- In Figure (i) and (ii) DE  ||  BC., Find EC in (i) and AD in (iii) (i)    Let EC= x cm  Given :- DE  ||  BC, therefore using Thales Theorem, we have AD/DB = AC/EC ➱ 1.5/3=1/x  ➱  x=(3*1)/1.5 =2 Hence, EC=2. (ii)              Let AD= x cm  Given :- DE  ||  BC, therefore using Thales Theorem, we have AD/DB= AC/EC ➱ x / 7.2=1.8 / 5.4 ➱ x=(1.8 * 7.2) / 5.4=2.4 Hence, AD=2.4     Question:-2    E and F are points on the sides PQ and PR respectively of a ΔPQR. For each of the following cases, state whether EF || QR.  (i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm (ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm (iii)PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm S olution:- (i) (i)    PE/EQ= 3.9/3=1.3 and PF/FR= 3.6/2.4=...

Example 1 . In a figure,PS/SQ =PT/TR and ∠PST = ∠PRQ. prove that PQR is an isosceles triangle. Solution :- it is given that  PS/SQ =PT/TR           so,   ST∥QR  ( converse of  Basic Proportionality Theorem ) Therefore,   ∠PST = ∠PQR (corresponding angles)........(1) Also,       it is given that                     ∠PST =∠PRQ...............(2) so,              ∠ PRQ= ∠PQR [ from (1) and (2)] Therefore,        PQ = PR (sides opposite the equal angles) i . e. ,  PQR is an isosceles triangle.                                                           

              EXERCISE 6.2 SUM 4.    In a figure, DE∥AC and DF∥ AE, prove that BE/FE=BE/EC. Solution:-  Given:-  DE∥AC  and DF∥ AE To Prove :-  BE/FE=BE/EC Proof:- In △ABC  DE∥AC  Because ( if a line is drawn parallel to one side of triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio .) BE/EC=BD/DA        .......(1) and, In △AEB DF∥ AE Because  ( if a line is drawn parallel to one side of triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio .) BF/FE= BD/DA            ......(2)     From (1) and (2)   BE/FE=BE/EC Hence proved 

 Imp rule use in this theorem is :- :- You can add the same value to each side of an equation without changing the meaning of the equation:-  For example:- Ax = By  Ax+1=By+1 Theorem 6.2:-  If a line divides any two sides of a triangle in the same ratio,then the line is parallel to the third side. Proof:- Given:- △ABC and a line DE intersecting AB at D and AC at E, Such that,     AD/DB = AE/EC  To Prove:-    DE∥BC Construction:- Draw DE'∥BC  Proof:- Since      DE'∥BC (By the Theorem  if a line is drawn parallel to one side of triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio . ) AD/DB=AE'/E'C.........(1)   and given that,  AD/DB=AE/EC....(2) From (1) and (2) AE'/E'C= AE/EC Adding 1 on both sides  (AE'/E'C)+1=( AE/EC)+1 (AE'+E'C)/E'C=( AE+EC)/EC  AC/E'C = AC/EC 1/E'C =1/EC EC=E'C ...

Imp points or results used in  Basic proportionality theorem or Thales theorem:- (i) Area of Triangle = 1/2 base* height Area of Triangle= 1/2 base*height                     =1/2 BC*AD (ii) Area of obtuse triangle =  In this figure CM is height of the triangle and AB is the base Area of triangle = 1/2 base* height                    =1/2 AB* CM (iii) Two triangles on the same base (or equal bases) and between the same parallels are equal in areas. (class 9th) There are two triangle in this figure △CDA and △CDB so,  ar(CDA)= ar(CDB) Theorem 6.1 if a line is drawn parallel to one side of triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio .   Proof  Given:-    triangle ABC in which a line l parallel to side BC intersects other two sides AB and AC at D and E respec...